728x90
반응형
알고리즘
: 문제를 해결하기위한 일련의 절차를 공식화한 형태로 표현한것.
좋은 알고리즘을 만들기 위해서는 다음과 같은 조건을 충족시켜야 한다.
- 입력 : 외부에서 제공되는 자료가 0개 이상 존재한다.
- 출력 : 적어도 2개 이상의 서로 다른 결과를 내어야 한다. 즉 모든 입력에 하나의 출력- 이 나오면 안 된다.
- 명확성 : 수행 과정은 명확하고 모호하지 않은 명령어로 구성되어야 한다.
- 유한성 : 유한 번의 명령어를 수행 후 유한 시간 내에 종료한다.
- 효율성 : 모든 과정은 명백하게 실행 가능(검증 가능)한 것이어야 한다.
알고리즘에 필요한 개념
- 시간 복잡도( 문제를 해결하는데 걸리는 시간과 입력의 함수관계)
- 자료구조
- 정렬

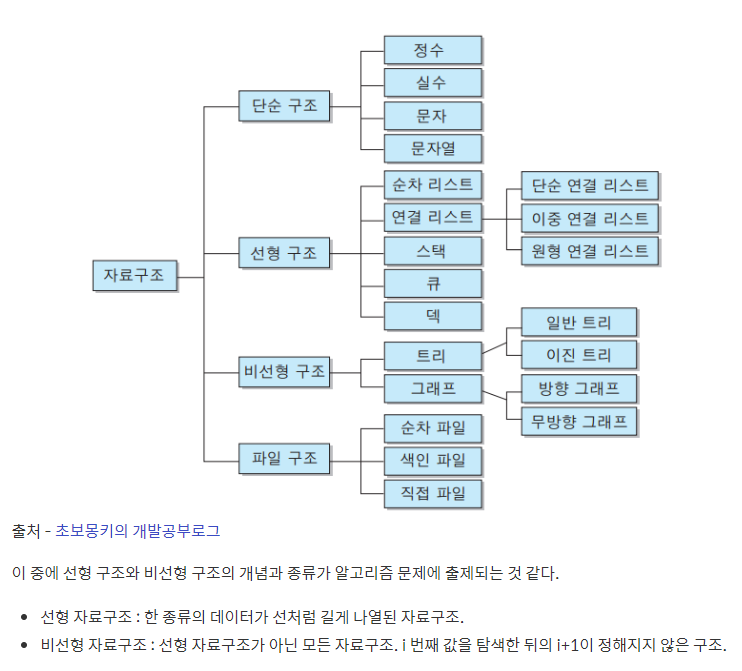
0. 알고리즘의 종류
- 검색알고리즘
- 재귀알고리즘
- 정렬알고리즘
1. 검색알고리즘
1-1) 선형검색(Liner Serch) : 복잡도 O(n)
- 배열을 검색하여 원하는 key값을 찾는 알고리즘.
- 배열의 맨앞부터 순차적으로 훑어가며 검색한다.
1-2) 이진검색(Binary Serch) : 복잡도 O(log(n))
- 정렬된 배열에서 원하는 key값을 찾는 알고리즘.
- 선형검색보다 빠르다.
2. 재귀알고리즘
2-1) 피보나치 수열 : 복잡도 O(2^n)
- 피보나치 수열은 다음과 같이 무한대로 이어지는 수열이다.
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.......
- 처음 시작하는 두개의 값은 각각 0과 1로 주어진다.
- 이후 스탭에서의 값은 앞의 두개의 값을 더한것과 같다.
- 재귀호출구조는 거듭되는 연산이 많아서 복잡하다.
2-2) 최대공약수(GCD) : 복잡도 O(log(n+m))
- 유클리드 알고리즘을 재귀호출 방법으로 사용할수 있다.
- a>=b라면 GCD(a,b) = GCD(b,r)이다. 여기서 r=a%b다. 즉 나머지.
- 즉, b가 0이 될때까지, 재귀호출은 반복한다. b가 0이되면, 최대공약수는 바로 a다.
2-3) 하노이의 탑알고리즘
- 이미 알아본 방법으로 원반 n-1개를 옮긴다.(재귀호출)
- 이미 알아본 방법으로 마지막 원반을 옮긴다.(재귀호출)
3. 정렬알고리즘
3-1) 선택정렬(Selection Sort) : 복잡도 O(n^2)
- 리스트안에 있는 자료들(소->대) 순서로 나열하려고한다.
- 가장 단순한 정렬이지만, 많이 비교하므로 복잡도가 높다.
- 첫번째 값을 가져올때 n-1회 비교하여 최솟값을 결과리스트에 가져온다.
- 두번째 값을 가져올때 n-2회 비교하여 최솟값을 결과리스트에 가져온다.
- 반복한다. 즉, 전체 비교횟수는 n(n-1)/2 다.
3-2) 삽입정렬(Insertion Sort) : 복잡도 O(n)~ O(n^2)의 사이
- 입력 리스트가 이미 정렬에 가까운 상태라면 복잡도는 낮아진다.
- 일반적으로 선택정렬과 유사한 성능을 가진다.
- 자료가 담긴 리스트에서 순차적으로 값을 가져온다. 첫째값은 그대로 가져옴.
- 두번째 값을 가져와 결과리스트와 비교후 위치를 정한다.
- 반복한다.
3-3) 병합정렬(Merge Sort) : 복잡도 O(log(n))
- 재귀호출을 사용하는 정렬
- 분할정복 방법의 알고리즘이다.
- 자료가 담긴 리스트를 가운데 기준으로 두개로 쪼갠다.-> 각 리스트에 첫값을 비교후 작은것을 골라 결과 리스트로 옮김
- 이전스텝 반복(재귀호출)
3-4) Quick Sort : 복잡도 O(log(n))
- 재귀호출을 사용하는 정렬
- 분할정복 방법의 알고리즘이다.
- 병함정렬과는 다르게 특정값을 피봇으로 정해서 입력리스트를 쪼갠다.
- 피봇보다 작은값은 리스트a, 큰값을 리스트b로 담는다.
- 두개의 a,b리스트에 재귀호출을 적용해서 정렬된 리스트로 만든다. (샌드위치 마냥,,)
3-5) Bubble Sort : 복잡도 O(n^2)
- 리스트를 훑어가며 인접한 값 두개씩 비교해서 정렬
- 더 이상 위치 변경이 필요없을때 까지 반복한다.
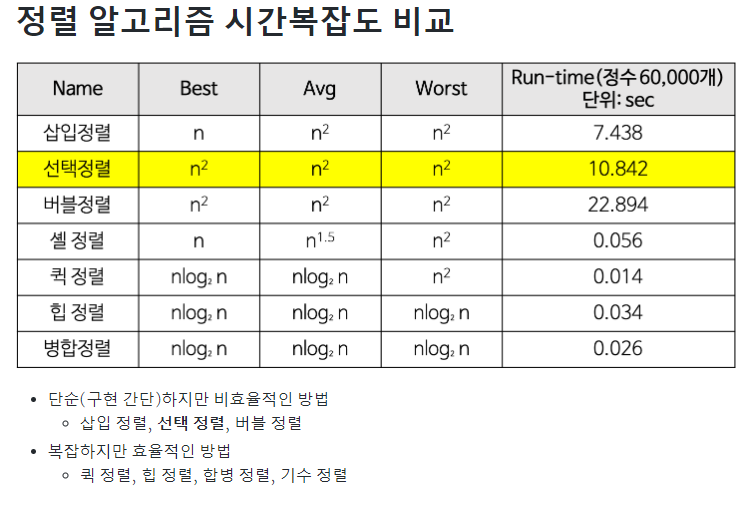
참고한곳 :
[출처] https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html (알고리즘 시간복잡도 표)
728x90
반응형
댓글